Recently, I was thinking about how many of the nontrivial problems that I run into with software engineering boil down to a few simple problems. Just look at any book on algorithms, and the majority of them will be some variation on sorting or searching collections. Google exists because the question of “what documents contain these phrases?” is a genuinely hard problem to solve (okay, that is vastly simplifying the enormous scope of Google’s product, but the basic idea still holds).
What is Topological Sorting?
One of these common problems that I have run into again and again over the course of my career is topologically sorting the nodes of a dependency graph. In other words, given some directed acyclic graph - think software packages that can depend on other software packages or tasks within a large company project - sort them such that no item in the list depends on anything that comes later in the list. Let’s imagine that we are making a cake, and before we can get started, we need some ingredients. Let’s simplify things and say we just need eggs and flour. Well, to have eggs, we need chickens (believe me, I’m resisting the urge to make a joke here), and to have flour, we need grain. Chickens also need grain for feed, and grain needs soil and water to grow in. If we consider the graph that expresses all of these dependencies, it looks something like this:
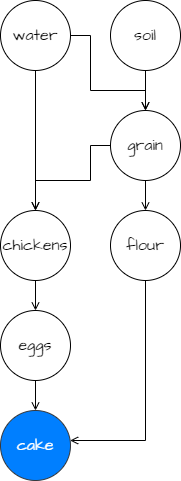
One possible topological order of this graph is:
[]string{"soil", "water", "grain", "chickens", "flour", "eggs", "cake"}
However, there are other possible sort orders that maintain topological ordering:
[]string{"water", "soil", "grain", "flour", "chickens", "eggs", "cake"}
We could also put the flour after the eggs, since the only thing that depends on eggs is cake. Since we can rearrange the items, we could also fulfill some of them in parallel while maintaining that no item appears before anything that depends on it. For example, by adding a level of nesting, we can indicate that everything within an inner slice is independent of anything else in that slice:
[][]string{
{"soil", "water"},
{"grain"},
{"chickens", "flour"},
{"eggs"},
{"cake"},
}
From this graph, we get a nice “execution plan” for how to prepare the dependencies for a cake. First, we need to find some soil and water. Next, we grow grain. Then, we simultaneously raise some chickens and make flour. Next, we collect the eggs. Then finally, we can make our cake! That may seem like a lot of work for petit fours, but good things take time.
Building a Dependency Graph
Now that we understand what we are trying to do, let’s think about how to write some code that is able to build this sort of dependency list. We will certainly need to keep track of the elements themselves, and we will need to keep track of what depends on what. In order to make both “What depends on X?” and “What does X depend on?” efficient, we will track the dependency relationship in both directions.
We have enough of an idea of what we need to start writing some code:
// A node in this graph is just a string, so a nodeset is a map whose
// keys are the nodes that are present.
type nodeset map[string]struct{}
// depmap tracks the nodes that have some dependency relationship to
// some other node, represented by the key of the map.
type depmap map[string]nodeset
type Graph struct {
nodes nodeset
// Maintain dependency relationships in both directions. These
// data structures are the edges of the graph.
// `dependencies` tracks child -> parents.
dependencies depmap
// `dependents` tracks parent -> children.
dependents depmap
// Keep track of the nodes of the graph themselves.
}
func New() *Graph {
return &Graph{
dependencies: make(depmap),
dependents: make(depmap),
nodes: make(nodeset),
}
}
This data structure should suit our purposes, since it holds all of the information we need: nodes, “depends-on” edges, and “depended-on-by” edges. Let’s think now about creating the API for adding new dependency relationships to the graph. All we need is a method for declaring that some node depends on another, like so: graph.DependOn("flour", "grain"). There are a couple of cases that we want to explicitly disallow. First, a node cannot depend on itself, and second, if flour depends on grain, then grain must not depend on flour, otherwise we would create an endless dependency cycle. With that, let’s write the Graph.DependOn() method.
func (g *Graph) DependOn(child, parent string) error {
if child == parent {
return errors.New("self-referential dependencies not allowed")
}
// The Graph.DependsOn() method doesn't exist yet.
// We'll write it next.
if g.DependsOn(parent, child) {
return errors.New("circular dependencies not allowed")
}
// Add nodes.
g.nodes[parent] = struct{}{}
g.nodes[child] = struct{}{}
// Add edges.
addNodeToNodeset(g.dependents, parent, child)
addNodeToNodeset(g.dependencies, child, parent)
return nil
}
func addNodeToNodeset(dm depmap, key, node string) {
nodes, ok := dm[key]
if !ok {
nodes = make(nodeset)
dm[key] = nodes
}
nodes[node] = struct{}{}
}
This will effectively add a dependency relationship to our graph once we implement Graph.DependsOn(). We could very easily tell whether a node depends on some other node directly, but we also want to know whether there is a transitive dependency. For example, since flour depends on grain, and grain depends on soil, flour depends on soil as well. This will require us to get the direct dependencies of a node, then for each of those dependencies, get its dependencies and so on until we stop discovering new dependencies. In computer science terms, we are computing a fixpoint to find the transitive closure of the “DependsOn” relation on our graph.
func (g *Graph) DependsOn(child, parent string) bool {
deps := g.Dependencies(child)
_, ok := deps[parent]
return ok
}
func (g *Graph) Dependencies(child string) nodeset {
if _, ok := g.nodes[root]; !ok {
return nil
}
out := make(nodeset)
searchNext := []string{root}
for len(searchNext) > 0 {
// List of new nodes from this layer of the dependency graph. This is
// assigned to `searchNext` at the end of the outer "discovery" loop.
discovered := []string{}
for _, node := range searchNext {
// For each node to discover, find the next nodes.
for nextNode := range nextFn(node) {
// If we have not seen the node before, add it to the output as well
// as the list of nodes to traverse in the next iteration.
if _, ok := out[nextNode]; !ok {
out[nextNode] = struct{}{}
discovered = append(discovered, nextNode)
}
}
}
searchNext = discovered
}
return out
}
Sorting The Graph
Now that we have a graph data structure, we can think about how to get the nodes out in a topological ordering. If we can discover the leaf nodes - that is, nodes that themselves have no dependencies on other nodes - then we can repeatedly get the leaves and remove them from the graph until the graph is empty. On the first iteration we will find the elements that are independent, then on each subsequent iteration, we will find the nodes that only depended on elements that have already been removed. The end result will be a slice of independent “layers” of nodes that are sorted topologically.
Getting the leaves of the graph is simple. We just need to find that nodes that have no entry in dependencies. This means that they do not depend on any other nodes.
func (g *Graph) Leaves() []string {
leaves := make([]string, 0)
for node := range g.nodes {
if _, ok := g.dependencies[node]; !ok {
leaves = append(leaves, node)
}
}
return leaves
}
The final piece of the puzzle is actually computing the topologically sorted layers of the graph. This is also the most complex piece. The general strategy that we will follow is to iteratively collect the leaves and remove them from the graph until the graph is empty. Since we will be mutating the graph, we want to make a clone of it so that the original graph is still intact after we perform the sort, so we’ll go ahead and implement that clone:
func copyNodeset(s nodeset) nodeset {
out := make(nodeset, len(s))
for k, v := range s {
out[k] = v
}
return out
}
func copyDepmap(m depmap) depmap {
out := make(depmap, len(m))
for k, v := range m {
out[k] = copyNodeset(v)
}
return out
}
func (g *Graph) clone() *Graph {
return &Graph{
dependencies: copyDepmap(g.dependencies),
dependents: copyDepmap(g.dependents),
nodes: copyNodeset(g.nodes),
}
}
We also need to be able to remove a node and all edges from a graph. Removing the node is simple, as is removing the outbound edges from each node. However, the fact that we keep track of every edge in both directions means that we have to do a little extra work to remove the inbound records. The strategy that we will use to remove all edges is as follows:
- Find node
A’s entry independents. This gives us the set of nodes that depend onA. - For each of these nodes, find the entry in
dependencies. RemoveAfrom thatnodeset. - Remove node
A’s entry independents. - Perform the inverse operation, looking up node
A’s entry independencies, etc.
With the help of a small utility that allows us to remove an node from a depmap entry, we can write the method that completely removes a node from the graph.
func removeFromDepmap(dm depmap, key, node string) {
nodes := dm[key]
if len(nodes) == 1 {
// The only element in the nodeset must be `node`, so we
// can delete the entry entirely.
delete(dm, key)
} else {
// Otherwise, remove the single node from the nodeset.
delete(nodes, node)
}
}
func (g *Graph) remove(node string) {
// Remove edges from things that depend on `node`.
for dependent := range g.dependents[node] {
removeFromDepmap(g.dependencies, dependent, node)
}
delete(g.dependents, node)
// Remove all edges from node to the things it depends on.
for dependency := range g.dependencies[node] {
removeFromDepmap(g.dependents, dependency, node)
}
delete(g.dependencies, node)
// Finally, remove the node itself.
delete(g.nodes, node)
}
Finally, we can implement Graph.TopoSortedLayers():
func (g *Graph) TopoSortedLayers() [][]string {
layers := [][]string{}
// Copy the graph
shrinkingGraph := g.clone()
for {
leaves := shrinkingGraph.Leaves()
if len(leaves) == 0 {
break
}
layers = append(layers, leaves)
for _, leafNode := range leaves {
shrinkingGraph.remove(leafNode)
}
}
return layers
}
This method clearly outlines our strategy for topologically sorting the graph:
- Clone the graph so that we can mutate it.
- Repeatedly collect the leaves of the graph into a “layer” of output.
- Remove each layer once it is collected.
- When the graph is empty, return the collected layers.
Now we can go back to our original cake-making problem to make sure that our graph solves it for us:
package main
import (
"fmt"
"strings"
"github.com/kendru/darwin/go/depgraph"
)
func main() {
g := depgraph.New()
g.DependOn("cake", "eggs")
g.DependOn("cake", "flour")
g.DependOn("eggs", "chickens")
g.DependOn("flour", "grain")
g.DependOn("chickens", "grain")
g.DependOn("grain", "soil")
g.DependOn("grain", "water")
g.DependOn("chickens", "water")
for i, layer := range g.TopoSortedLayers() {
fmt.Printf("%d: %s\n", i, strings.Join(layer, ", "))
}
// Output:
// 0: soil, water
// 1: grain
// 2: flour, chickens
// 3: eggs
// 4: cake
}
All of that work was not exactly a piece of cake, but now we have a dependency graph that can be used to topologically sort just about anything. You can find the full code for this post on GitHub. There are some notable limitations to this implementation, and I would like to challenge you to improve it so that it can:
- Store nodes that are not simple strings
- Allow nodes and edges/dependency information to be added separately
- Produce string output for debugging
I hope you enjoyed this tutorial! Please let me know what you would like me to cover next.